Bayesian sparse hierarchical model for image denoising

Abstract

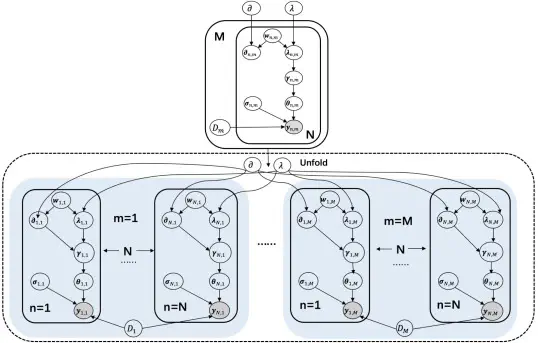
Sparse models and their variants have been extensively investigated, and have achieved great success in image denoising. Compared with recently proposed deep-learning-based methods, sparse models have several advantages:(1) Sparse models do not require a large number of pairs of noisy images and the corresponding clean images for training. (2) The performance of sparse models is less reliant on the training data, and the learned model can be easily generalized to natural images across different noise domains. In sparse models, L0 norm penalty makes the problem highly non-convex, which is difficult to be solved. Instead, L1 norm penalty is commonly adopted for convex relaxation, which is considered as the Laplacian prior from the Bayesian perspective. However, many previous works have revealed that L1 norm regularization causes a biased estimation for the sparse code, especially for high-dimensional data, e.g., images. In this paper, instead of using the L1 norm penalty, we employ an improper prior in the sparse model and formulate a hierarchical sparse model for image denoising. Compared with other competitive methods, experiment results show that our proposed method achieves a better generalization for images with different characteristics across various domains, and achieves state-of-the-art performance for image denoising on several benchmark datasets.